什么是标准偏差，标准偏差计算方法

       我们在读书的时候都会学习数学这门课程，即使很多人上了大学之后有的专业还是需要学数学的。但是很多人觉得复杂的数学在我们日常生活中并不实用。简单的加减乘除就已经够了，其实学习数学并不是简单的在生活中运用，更是要学习理解数学的思维模式，锻炼能够思考复杂数学问题的能力。在数学中有很多专业名词，比如标准偏差，标准偏差的结果可以看出一组数据是否稳定，不过有的小伙伴还不清楚如何计算标准偏差，下面小编就给大家带来标准偏差计算公式。

   

什么是标准偏差

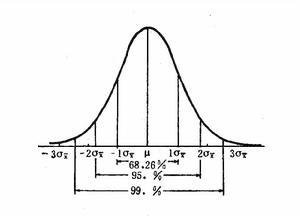
1. 标准偏差(Standard Deviation)是统计学中用来描述数据分布的一项指标。它可以衡量数据集的离散程度和波动程度，即数据点与均值之间的偏差。标准偏差越大，代表数据的差异性越高;标准偏差越小，代表数据的相似性越高。

2. 标准偏差的计算步骤相对简单。首先，需要计算数据的平均值(均值)。然后，将每个数据点与平均值的差值平方，再将这些差值平方的和除以数据点的个数。最后，将结果开根号得到标准偏差。

3. 具体计算步骤如下：

1) 首先，计算数据的平均值。将所有数据相加，然后除以数据的个数即可。

2) 然后，计算每个数据点与平均值的差值。将每个数据点减去平均值，得到差值。

3) 接下来，把每个差值平方。将每个差值乘以自己，得到平方值。

4) 再将平方值相加。把所有的平方值相加，得到总和。

5) 最后，求平均数的平方根。将总和除以数据的个数，然后开根号即可得到标准偏差。

4. 通过计算标准偏差，我们可以更好地了解数据的分布情况。标准偏差越大，说明数据的离散程度越高，波动范围也越大;标准偏差越小，说明数据的离散程度越小，波动范围也越小。

5. 总而言之，标准偏差是用来衡量数据分布离散程度的一项指标。通过计算数据点与均值之间的偏差，我们可以获得数据的波动范围和差异性。标准偏差的计算步骤相对简单，只需计算平均值、差值平方和、平方和总和，然后开根号即可得到结果。标准偏差的大小可以帮助我们判断数据的离散程度和相似性。